L’ equazione di Hammett è usata per spiegare le interazioni intramolecolari, elettroniche o steriche, e per correlare l’influenza dei sostituenti sulle velocità delle reazioni organiche
Nel 1935 il chimico statunitense Louis Plack Hammett espose un criterio per correlare le costanti di velocità di reazione relative a serie omogenee di reazioni organiche in soluzione. Tale criterio offre la possibilità di predire la costante di velocità di reazione quando non sono disponibili dati cinetici.
L’equazione di Hammett è quindi utilizzata nell’indagine sui meccanismi di reazione fornendo una logica a molti modelli di reazione e monitorare l’entità dello sviluppo di carica nel complesso attivato.
Egli confrontò gli effetti della variazione dei sostituenti nelle posizioni meta e para di un anello benzenico di una serie di acidi benzoici sulla costante acida Ka e sulla velocità di idrolisi degli esteri corrispondenti. Se un sostituente è legato alla posizione meta o para di un anello benzenico, cambierà la capacità dell’anello aromatico di donare o ritirare elettroni rispetto al benzene stesso.
Utilizzando una reazione modello ovvero la ionizzazione degli acidi benzoici, la capacità di un sostituente di modificare la capacità di donazione o di attrazione di elettroni del gruppo fenilico e quindi di influenzare tale reazione può essere definita quantitativamente dall’equazione di Hammett.
L’equazione di Hammett afferma quindi che questi stessi sostituenti avranno effetti sull’equilibrio o sulle costanti di velocità per qualsiasi altra reazione che sia linearmente parallela a quelle della ionizzazione dell’acido benzoico. La costante di proporzionalità cioè la pendenza della linea varierà con la particolare reazione in studio, ma la sua grandezza rivela il grado di sensibilità della reazione agli effetti sostituenti.
Diagramma dell’equazione di Hammett
Se si riporta su un diagramma il logaritmo della costante di velocità in ordinata e il logaritmo della costante di dissociazione K in ascissa si ottiene l’andamento mostrato in figura:
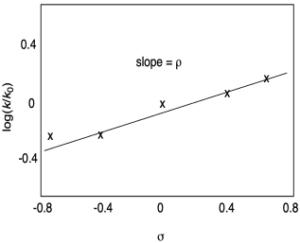
In tutti i casi da lui presi in considerazione Hammett riscontrò sempre l’esistenza di una relazione lineare del tipo:
ln k = ρ ln Ka + A (1)
tra il logaritmo della costante di velocità k e la costante di equilibrio dell’acido benzoico Ka.
Questa espressione può essere generalizzata eliminando la costante A. Se si prende come riferimento una generica costante di velocità e la corrispondente costante di ionizzazione si ha:
A = ln k° – ρ ln K°a (2)
Da cui sostituendo ad A il valore ricavato nella (2)
ln k = ρ ln Ka + ln k° – ρ ln K°a
ovvero:
ln k – ln k° = ρ(ln Ka – ln K°a) (3)
dove ρ è una costante che dipende solo dalla reazione considerata e dalle condizioni sperimentali in cui essa viene condotta.
Il termine al secondo membro non è altro che la differenza di logaritmi delle due costanti di dissociazione di due acidi benzoici sostituiti. Tale differenza, che dipende solo dai sostituenti presenti e non dalla reazione a cui essi prendono parte, viene normalmente indicata con σ:
σ = ln Ka – ln K°a (4)
l’equazione (3) diventa:
ln k – ln k° = ρ σ (5)
la relazione (3) risulta utile se sono noti almeno due valori delle costanti di equilibrio Ka e K°a e i due corrispondenti valori della costante di velocità k e k°.
Il valore di σ può essere così calcolato dalla (4) e il valore di ρ si ottiene dalla relazione (5):
ρ = ln k – ln k°/ σ
Poiché il logaritmo della costante di equilibrio è proporzionale alla variazione di energia libera standard, mentre sulla base della teoria dello stato di transizione il logaritmo della velocità di reazione risulta proporzionale all’energia libera di attivazione, la (3) può essere riscritta come:
δΔG≠ = α δΔG°
dove δΔG≠ è la differenza dell’energia libera di attivazione per due reazioni simili mentre δΔG° è la differenza dei valori delle variazioni di energia libera standard delle stesse reazioni e α è un fattore di proporzionalità. La relazione precedente implica l’esistenza di una relazione lineare fra le energie libere di reazione ( linear free relationship o LFER)
